(Doesn't show coarsest grid)
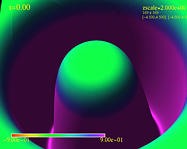
X-Y Plane; Smooth Mesh (1MB MPG)

Y-Z Plane; Smooth Mesh (1MB MPG)
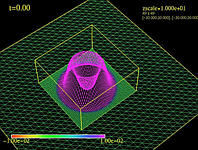
1D Cuts through X and Z axes; (6MB MPG)
| Home | · | Papers | · | Research Interests | · | Movies | · | Teaching | · | Personal |
| Toroid (Doesn't show coarsest grid) |

X-Y Plane; Smooth Mesh (1MB MPG) |

Y-Z Plane; Smooth Mesh (1MB MPG) 
1D Cuts through X and Z axes; (6MB MPG) |
 Movie of chi with
bounding boxes on the various grids (z=0 slice).
Movie of chi with
bounding boxes on the various grids (z=0 slice).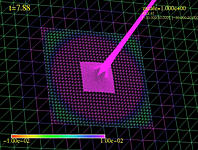 Movie of the near-critical energy density (z=0 slice).
Movie of the near-critical energy density (z=0 slice).One other thing about the above. In this nlsm model, I use a generalized hedgehog ansatz which requires somewhere that the field goes to zero. I fix the field to be zero at the origin, and that's why you see the zero point at the origin in the above.
| Last updated April 15, 2002. | Copyright 2000 S.L. Liebling |
| (home) | Research Supported by NSF |